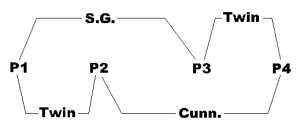

The first example is quite simple [5,7
11,13].
These groups of prime numbers that I call " BiTwins "
are rather easy to find (and are somewhat aesthetically pleasing!). Indeed,
because of their connections, the constituent numbers have simple linear
forms. A small calculation shows that p1 is form 30a-1 (for p1>5), p2
= 30a+1, p3 = 60a-1, p4 = 60a+1. In base 10 representation their final digits
must be 9 and 1.
The following examples can be found immediately:
[29,31 59,61] [659,661
1319,1321] [809,811 1619,1621]
[2129,2131 4259,4261] ... ...
... [2003999,2004001 4007999,4008001] ... ...
Generalization :
It is possible to continue the process to obtain a chain of several " BiTwins
" (perhaps as long as one wants), according to the diagram below:
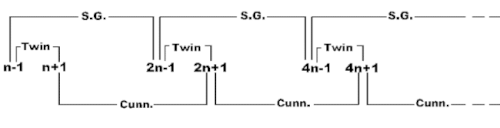
It will be noted that one obtains Cunningham chains of
both first and second kinds of length = (number of BiTwin 'links' +1). The
calculations yield simple linear forms for n: 210*a (for 2 links)
2310*a+0,420,1890 (for 3 links) etc...
For 2 links smallest is: [211049,211051 422099,422101 844199,844201]
For 3 links smallest is: [253679,253681 507359,507361 1014719,1014721 2029439,2029441]
...
Questions arise:
- is (30*a) easily decomposable in prime factors for n large?
- can p2 be put in the form k*2m+1 to be able to use Proth's theorem
of Proth? That is possible, but unfortunately seldom (10 times for
n<6*1010) :
| Rank | "BiTwins" k*2m+/-1 k*2m+1+/-1 |
| 1 | 855*210-1, 855*210+1 855*211-1, 855*211+1 |
| 2 | 5565*213-1, 5565*213+1 5565*214-1, 5565*214+1 |
| 3 | 4935*216-1, 4935*216+1 4935*217-1, 4935*217+1 |
| 4 | 6105*216-1, 6105*216+1 6105*217-1, 6105*217+1 |
| 5 | 735*220-1, 735*220+1 735*221-1, 735*221+1 |
| 6 | 31215*215-1, 31215*215+1 31215*216-1, 31215*216+1 |
| 7 | 47745*218-1, 47745*218+1 47745*219-1, 47745*219+1 |
| 8 | 80985*218-1, 80985*218+1 80985*219-1, 80985*219+1 |
| 9 | 50505*220-1, 50505*220+1 50505*221-1, 50505*221+1 |
| 10 | 54645*220-1, 54645*220+1 54645*221-1, 54645*221+1 |
| See Records |
- Can p2 be put in the p*2b3c5d+1 form with
p prime, in order to use a primality test (n-1) more general ? It is
also possible and the "BiTwins" are a lot more easy to find
( 197 pour n<107):
| Rank | "BiTwins" p*2b3c5d+-1 | p |
| 1 | 659,661 1319,1321 | 11 |
| 2 | 2129,2131 4259,4261 | 71 |
| 3 | 2549,2551 5099,5101 | 17 |
| 4 | 3329,3331 6659,6661 | 37 |
| 5 | 3389,3391 6779,6781 | 113 |
We can also find "BiTwins" of this form with p=1 (3 pour
n<109):
| Rank | "BiTwins" 2b3c5d+-1 | "BiTwins" 2b3c5d+-1 |
| 1 | 29,31 59,61 | 2.3.5-1, 2.3.5+1 22.3.5-1, 22.3.5+1 |
| 2 | 809,811 1619,1621 | 2.34.5-1, 2.34.5+1 22.34.5-1, 22.34.5+1 |
| 3 | 431999999,432000001 863999999,864000001 | 210.33.56-1, 210.33.56+1 211.33.56-1, 211.33.56+1 |
Some other numerical results: :
| Rank | "BiTwins" 1 link |
| 1 | 5,7 11,13 |
| 2 | 29,31 59,61 |
| 3 | 659,661 1319,1321 |
| 4 | 809,811 1619,1621 |
| 5 | 2129,2131 4259,4261 |
| 6 | 2549,2551 5099,5101 |
| 7 | 3329,3331 6659,6661 |
| 8 | 3389,3391 6779,6781 |
| 9 | 5849,5851 11699,11701 |
| 10 | 6269,6271 12539,12541 |
| See Records |
| Rank | "BiTwins" 2 links |
| 1 | 211049,211051 422099,422101 844199,844201 |
| 2 | 248639,248641 497279,497281 994559,994561 |
| 3 | 253679,253681 507359,507361 1014719,1014721 |
| 4 | 410339,410341 820679,820681 1641359,1641361 |
| 5 | 507359,507361 1014719,1014721 2029439,2029441 |
| 6 | 605639,605641 1211279,1211281 2422559,2422561 |
| 7 | 1121189,1121191 2242379,2242381 4484759,4484761 |
| 8 | 1138829,1138831 2277659,2277661 4555319,4555321 |
| 9 | 1262099,1262101 2524199,2524201 5048399,5048401 |
| 10 | 2162579,2162581 4325159,4325161 8650319,8650321 |
| See Records |
| Rank | "BiTwins" 3 links |
| 1 | 253679,253681 507359,507361 1014719,1014721 2029439,2029441 |
| 2 | 1138829,1138831 2277659,2277661 4555319,4555321 9110639,9110641 |
| 3 | 58680929,58680931 117361859,117361861 234723719,234723721 469447439,469447441 |
| 4 | 90895769,90895771 181791539,181791541 363583079,363583081 727166159,727166161 |
| See Records |
| n<= | "BiTwins" 1 link |
"BiTwins" 2 links |
"BiTwins" 3 links |
| 10 | 1 | 0 | 0 |
| 102 | 2 | 0 | 0 |
| 103 | 4 | 0 | 0 |
| 104 | 10 | 0 | 0 |
| 105 | 29 | 0 | 0 |
| 106 | 144 | 6 | 1 |
| 107 | 752 | 15 | 2 |
| 108 | 4390 | 52 | 4 |
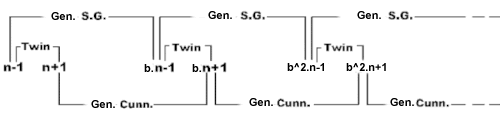
Generalized BiTwins :
If we replace the Cunningham chain of first and second kind respectively by
Generalized Cunningham chains we can have Generalized
BiTwins, according to the diagram below :